课程内容提要 ✌ #

• 1. 图论
  • 最小生成树   ✅
  • 最短路径    ✅
  • 网络与最大流量 ✅
• 2. 运筹方法
  • 线性规划    ✅
  • 动态规划    ✅✅✅
  • 预测与决策   ✅
• 3. 数学建模    ✅✅
  • 面积体积估算法

1 图论 #

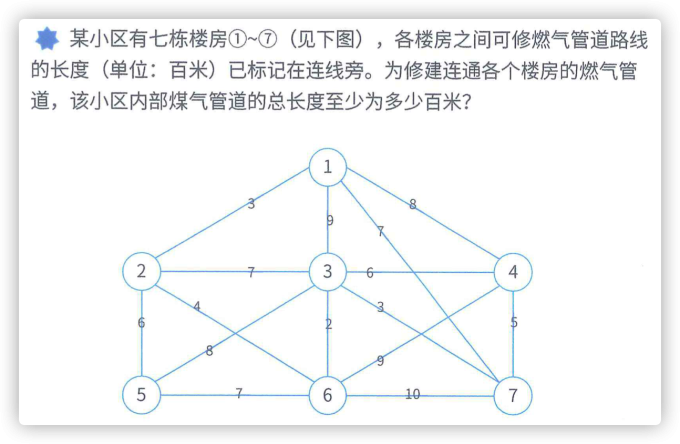
1.1 最小生成树 #

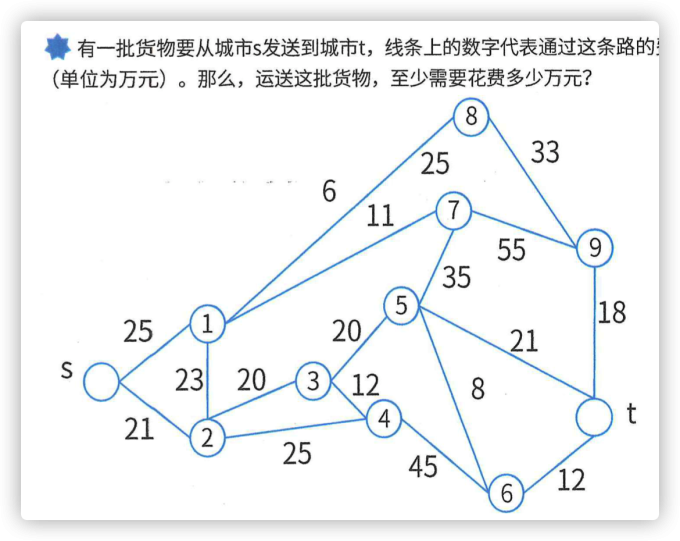
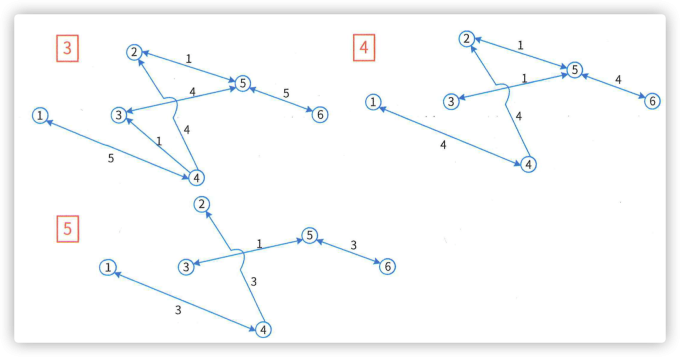
1.2 最短路径 #

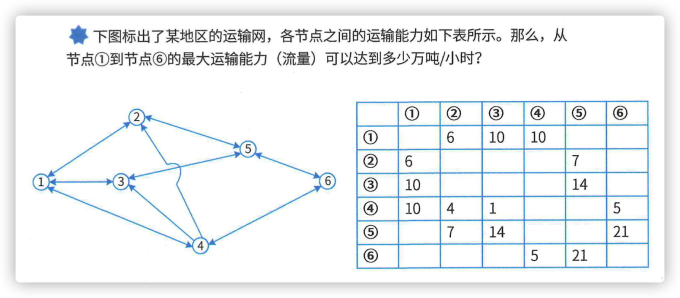
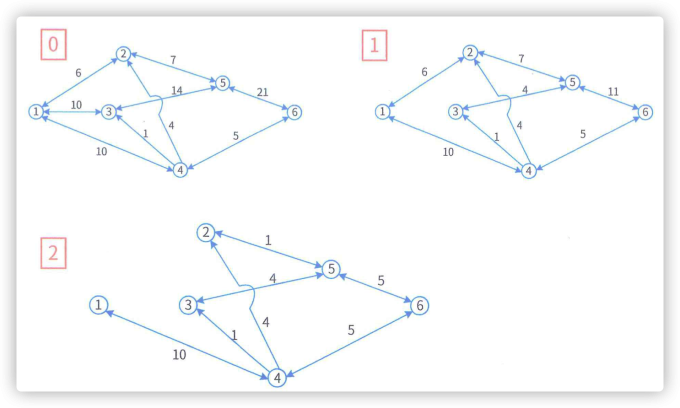
1.3 网络与最大流量 #

2 运筹方法 #

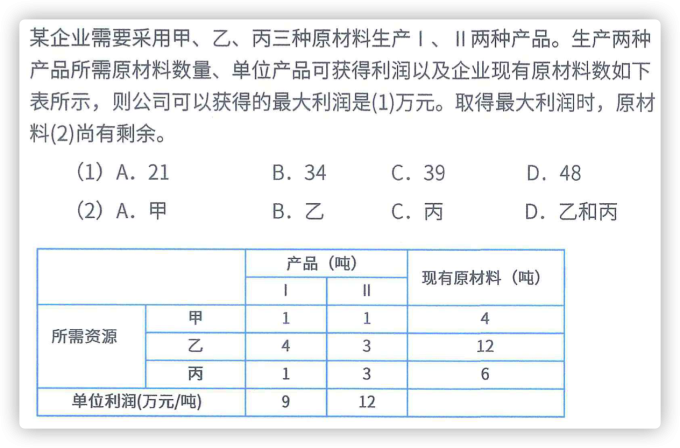
2.1 线性规划 #

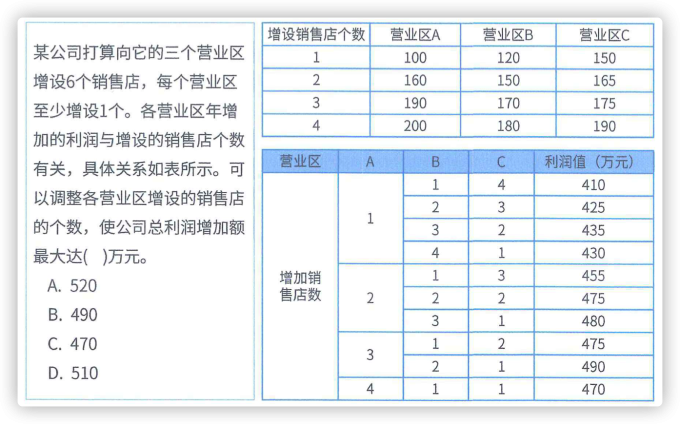
2.2 动态规划 #

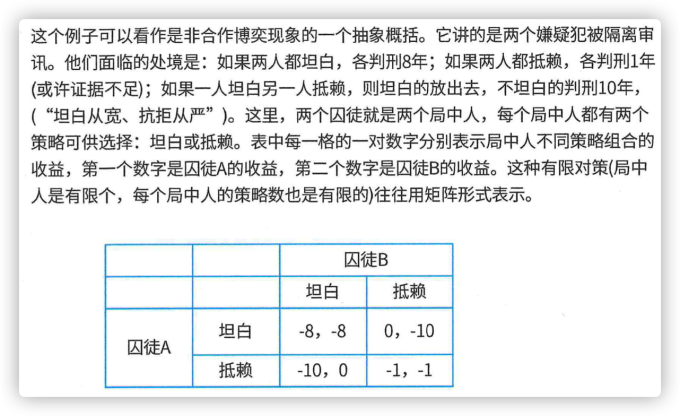
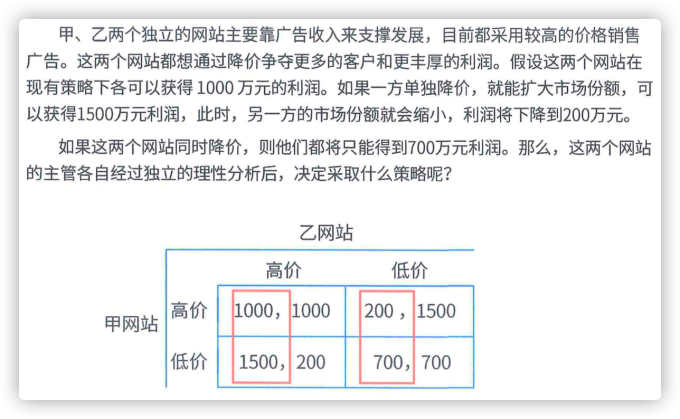
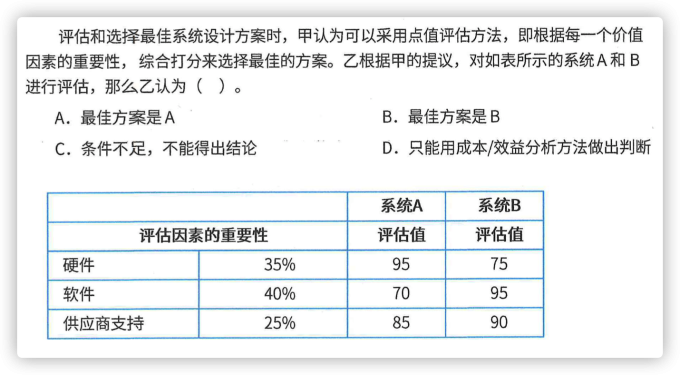
2.3 预测与决策 #

总结：乐观->大中取大，悲观->小中取大，后悔值->大中取小

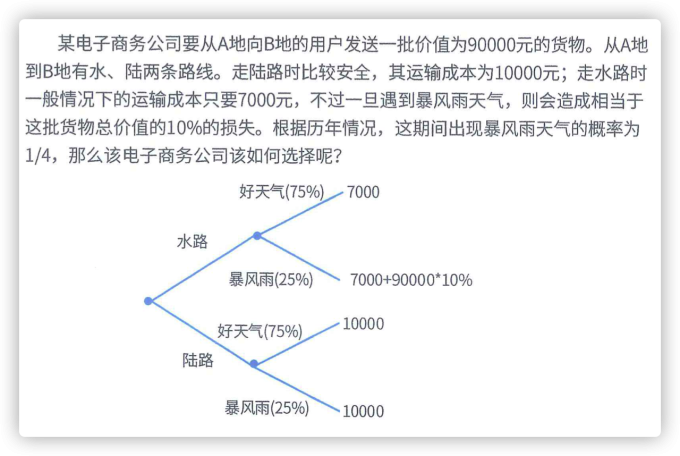
水路代价比较小

3 数学建模 #

  解决多数实际问题的关键是建立数学模型 (包括数学方程、数学公式、图形描述、符号表示等)。数学建模是对现实世界的一种近似的、简化的、易于求解的抽象描述。数学模型常需要忽略某些次要因素，以便易于近似求解过于简单的模型能准确性不足，为提高准确性，若建立过于复杂的模型，求解的难度就会增加。在简单性和准确性之间求得平衡是数学建模的一条原则。对同一问题可以建立多种数学模型。数学模型也常带有一些可变的参数。选用哪个模型，或选择什么样的参数，更能近似地解决实际问题，符合实际要求，这需要反复多次试验，根据求解失败的教训或用户的反馈意见逐步对模型进行修正或改进，逐步完善模型，并求得使用户满意，符合实际情况的结果。对一般的问题，并没有统一的、普适的模型评价标准，没有最好，只有更好，实践是检验真理的唯一标准。

  在对实际应用问题建立数学模型并求得结果后，还需要根据建模的目的和要求，利用相关知识，结合研究对象的特点，进行模型分析。模型分析工作主要包括模型的合理性分析、模型的误差分析和参数的灵敏性分析等，一般不包括模型的先进性分析。

3.1 面积体积估算法 #

  利用计算机的随机数来估算不规则的面积、体积。

课后习题 #

todo 数字与经济管理习题